Diferencia entre revisiones de «Escala lineal de frecuencia»
Sin resumen de edición |
m (Texto reemplazado: «<embed>https://www.youtube.com/watch?v=» por «{{video|») |
||
| (No se muestran 10 ediciones intermedias de 2 usuarios) | |||
| Línea 6: | Línea 6: | ||
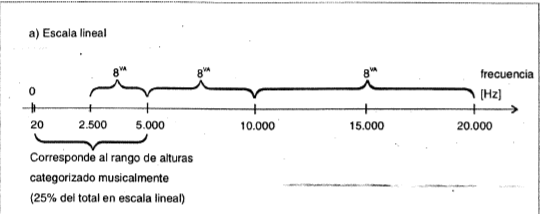
La escala lineal de frecuencia es la que demuestra el análisis de una señal que recorre en | La escala lineal de frecuencia es la que demuestra el análisis de una señal que recorre en [[Frecuencia]] (el parámetro inestable y físico del estimulo) y que queda de manera monótona en la [[Amplitud]](el parámetro fijo).De resolución constante que va en la escala desde el cero,en el rango audible de entre 20hz y 20 khz.([[Umbral de audibilidad]]) | ||
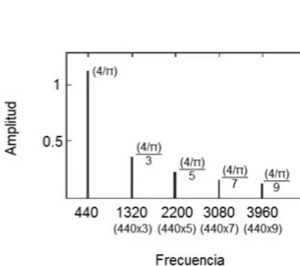
Aunque a intervalos mayores de variación de frecuencia son distintas las distancias en cuanto a la | Aunque a intervalos mayores de variación de frecuencia son distintas las distancias en cuanto a la [[Altura]](el rasgo perseptual), van disminuyendo.Luego de la fundamental la sucesión de los sonidos de la serie disminuyen en cuanto altura ,y en algunos casos se distinguen en forma de armónicos ,múltiplos enteros de la fundamental ([[serie armónica]]). | ||
Como se ve en el gráfico "Cada octava se extiende a través de un rango de frecuencias que es del doble del tamaño que el rango de frecuencias de la octava anterior" por ello la altura va disminuyendo al haber un aumento lineal de la frecuencia. | Como se ve en el gráfico "Cada octava se extiende a través de un rango de frecuencias que es del doble del tamaño que el rango de frecuencias de la octava anterior" por ello la altura va disminuyendo al haber un aumento lineal de la frecuencia. | ||
| Línea 15: | Línea 15: | ||
==='''''Ejemplo'''''=== | ==='''''Ejemplo'''''=== | ||
un claro ejemplo podría ser el adorno Glissando en un | un claro ejemplo podría ser el adorno [https://es.wikipedia.org/wiki/Glissando Glissando] en un violín , que demuestra una clara relación con el concepto ya que los sonidos aumentan en octavas ,demostrando un aumento en frecuencia y una clara disminución en altura. | ||
[https://upload.wikimedia.org/wikipedia/commons/6/6f/Violin_sounds_and_techniques.ogg glissando en violín al final] | [https://upload.wikimedia.org/wikipedia/commons/6/6f/Violin_sounds_and_techniques.ogg glissando en violín al final] | ||
{{video|BnTTrzClMkg&t=135s}} | |||
== '''''Referencias ''''' == | == '''''Referencias ''''' == | ||
| Línea 27: | Línea 28: | ||
* https://es.wikipedia.org/wiki/Serie_arm%C3%B3nica_(m%C3%BAsica) | * https://es.wikipedia.org/wiki/Serie_arm%C3%B3nica_(m%C3%BAsica) | ||
*https://es.wikipedia.org/wiki/Glissando | *https://es.wikipedia.org/wiki/Glissando | ||
*http://latecladeescape.com/h/2015/08/frecuencia-de-las-notas-musicales# | |||
Revisión actual - 10:42 25 jul 2019
| Definición Breve | análisis de la frecuencia que es variable con altura que disminuye |
|---|---|
| Tema | Altura y Espectro |
| Subtema | Escala lineal de frecuencia |
| Audio | <embed>glissando en violin al final</embed> |
Definición
La escala lineal de frecuencia es la que demuestra el análisis de una señal que recorre en Frecuencia (el parámetro inestable y físico del estimulo) y que queda de manera monótona en la Amplitud(el parámetro fijo).De resolución constante que va en la escala desde el cero,en el rango audible de entre 20hz y 20 khz.(Umbral de audibilidad) Aunque a intervalos mayores de variación de frecuencia son distintas las distancias en cuanto a la Altura(el rasgo perseptual), van disminuyendo.Luego de la fundamental la sucesión de los sonidos de la serie disminuyen en cuanto altura ,y en algunos casos se distinguen en forma de armónicos ,múltiplos enteros de la fundamental (serie armónica). Como se ve en el gráfico "Cada octava se extiende a través de un rango de frecuencias que es del doble del tamaño que el rango de frecuencias de la octava anterior" por ello la altura va disminuyendo al haber un aumento lineal de la frecuencia.
Ejemplo
un claro ejemplo podría ser el adorno Glissando en un violín , que demuestra una clara relación con el concepto ya que los sonidos aumentan en octavas ,demostrando un aumento en frecuencia y una clara disminución en altura.
Provided ID could not be validated.
Referencias
- Basso, Gustavo: Análisis Espectral. La transformada de Fourier en la Música, Editorial de la Universidad Nacional de La Plata, Buenos Aires, 2001.