Longitud de onda

Longitud de onda

[[File:|300px]]

Definición Breve	Es la distancia en la que se repite la misma forma de onda, como por ejemplo dos máximos de la misma.
Tema	Longitud de onda
Subtema	Ondas mecánicas sonoras, Otros tipos de ondas
Audio	<embed>Ejemplo</embed>

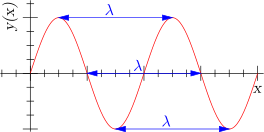
En el caso de una onda periódica, la longitud de un patrón de onda completo es la distancia entre una cresta y la siguiente, o de un valle al siguiente, o de cualquier punto al punto correspondiente en la siguiente repetición de la forma de onda. Llamamos a esta distancia longitud de onda, denotada con λ ( [ [ Λ | lambda ] ] ), letra griega. El patrón de onda viaja con rapidez constante "v" y avanza una longitud de onda λ en el lapso de un período, denotado "T". Por lo tanto se concluye que v=λ.T. En gran parte de los casos, la velocidad de propagación de la onda dependerá exclusivamente del medio en el que se propaga, por lo todas las ondas de cualquier longitud poseerán la misma rapidez, modificando su período para mantener la relación anterior constante.

Longitud de onda en ondas mecánicas sonoras

Uno de los ejemplos más usuales de ondas mecánicas, son las ondas sonoras. Sólo existe un pequeño espectro de longitud de onda en el que los humanos podemos percibir. Al igual que todas las ondas mecánicas, éstas necesitan un medio material para propagarse, este medio puede ser sólido, líquido o gaseoso; ordenados en orden decreciente con respecto a la velocidad de propagación en el medio. Para este tipo de ondas, se suele hablar de su frecuencia recordando que es la inversa del período y al mismo tiempo la relación entre período y longitud de onda. El oído humano normal puede oír entre frecuencias de 20 y 20.000 Hz. Las ondas que poseen una frecuencia inferior a la audible se denominan infrasónicas y las superiores ultrasónicas. Las ondas sonoras se propagan a través del aire o cualquier medio elástico en forma de vibraciones producidas por variaciones de presión. Estas vibraciones son captadas por el oído y a través de un proceso que involucra el tímpano, la cóclea y las células ciliadas, la energía mecánica se transforma en impulsos eléctricos que el nervio auditivo envía al cerebro para que éste lo procese. A mayor frecuencia, el cerebro asocia el sonido con un tono más agudo, de lo contrario el sonido será percibido como más grave.

Otros tipos de onda

Longitud de onda en ondas electromagnéticas

Al igual que en las ondas mecánicas sonoras, dentro del espectro electromagnético visible, a partir de la longitud de onda se pueden separar las ondas que vemos con distintos colores:

• rojo 618-780 nm
• anaranjado 581-618 nm
• amarillo 570-581 nm
• verde 497-570 nm
• cian 476-497 nm
• azul 427-476 nm
• violeta 380-427 nm

Siendo 1 nm = 10−9 m

Una aplicación clara son los lasers. Un láser es una fuente de haces coherentes y monocromáticos, es decir de una sola frecuencia, por lo que logra una luz de un color particular. La versión más barata es la de color rojo que emite a 670nm.

Longitud de onda en mecánica cuántica

En la mecánica clásica, se parte del supuesto que hay una diferenciación clara entre una onda y una partícula. A principios del siglo XX el físico francés Louis-Victor de Broglie introdujo por primera vez la idea de dualidad onda-partícula. La conclusión directa de ésta teoría es que para todo cuerpo en movimiento existe una onda asociada, cuya longitud de onda se puede calcular a partir de la fórmula

λ =h/p

Siendo h la Constante de Planck 6.62606957(29) ×10 ^-34 [ [ Julio (unidad) | J ] ] × [ [ segundo| s ] ] y p la cantidad de movimiento (p=m.v)

Ésta teoría se aplica en la actualidad para explicar el comportamiento de por ejemplo electrones y más importante, para fotones de luz. Al realizar los cálculos en cuerpos grandes, el valor de la longitud de onda toma un valor tan pequeño que no tiene un significado físico real ni es posible detectar sus efectos.

Referencias

• Wikipedia - espectroscopia
• Zemansky, Sears. Física Universitaria, Vol 1.
• Wikipedia - onda sonora
• Wikipedia - dualidad onda de Broglie y ondas de materia
• Medel - Audición