Diferencia entre revisiones de «Onda triangular»
Sin resumen de edición |
Sin resumen de edición |
||
| Línea 19: | Línea 19: | ||
<embedvideo service="youtube">https://https://www.youtube.com/watch?v=lYrcBkX45S8</embedvideo> | <embedvideo service="youtube">https://https://www.youtube.com/watch?v=lYrcBkX45S8</embedvideo> | ||
<embedvideo service="youtube">https://www.youtube.com/watch?v=Q3oItpVa9fs</embedvideo> | |||
==Referencia== | ==Referencia== | ||
Revisión del 00:01 22 oct 2016
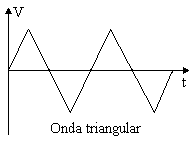
Onda triangular
| Definición Breve | Contiene todos los armónicos impares de la fundamental y su amplitud decrece a medida que aumenta la frecuencia. |
|---|---|
| Tema | Señal |
| Subtema | Onda |
| Audio | <embed>[1]</embed> |
Definición
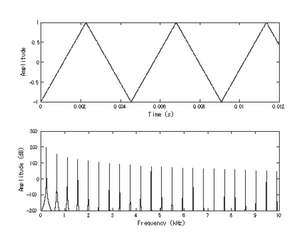
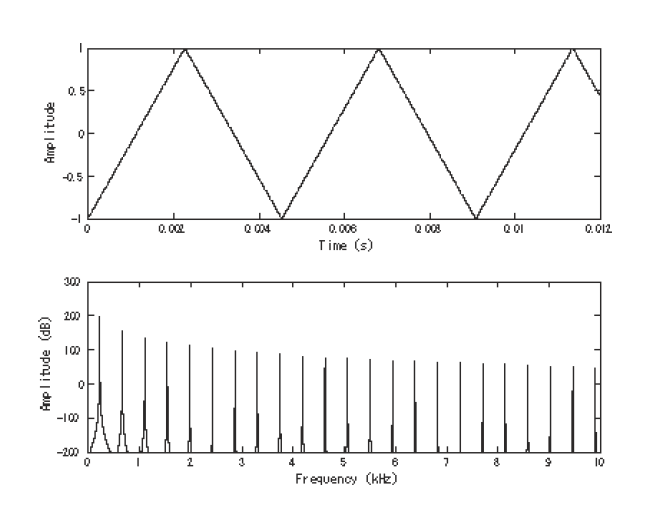
La onda "triangular" es un tipo de señal periódica (ver Señal estacionaria periódica/cuasi periódica). Su forma cuenta con dos pendientes lineales y no es tan armónicamente rica como la onda diente de sierra, de modo que contiene sólo armónicos impares. Su amplitud decrece con el inverso del cuadrado del número armónico correspondiente, así la amplitud del armónico 5 será de 1/5*5= 1/25. Por lo tanto, el espectro es muchas más simple que el de la onda cuadrada.
Sonido
Referencia
- http://cmm.cenart.gob.mx/tallerdeaudio/cursos/cursomusica_computadora/12musicaporcomputadora-sintesis.pdf
- http://nosolominimal.webnode.es/news/introduccion-a-los-sonidos-sintetizados/
- https://www.uam.es/personal_pdi/ciencias/evelasco/docencia/HOJA1a/res1/node8.html
- Gustavo Basso (2001), "Análisis espectral, la transformada de Fourier en la música". Buenos Aires, Argentina. Editorial: Ediciones al margen.