Relación entre Δt muy corto y altura espectral
| Definición Breve | Relación entre pulsos de distinta corta y sus espectros de Frecuencia |
|---|---|
| Tema | Relación entre Δt muy corto y altura espectral |
| Subtema | Principio de indeterminación |
| Audio | <embed>[1]</embed> |
Límite temporal y ancho de banda
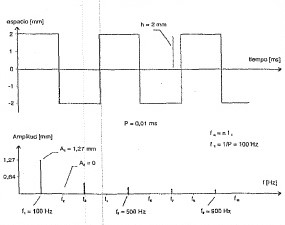
Para vincular una señal limitada en el tiempo con su representación espectral. Consideramos que la figura cuadrada de la figura a que reproducimos con ligeras variaciones de figura 2-a, a la derecha del gráfico temporal se puede ver el espectro de amplitud que le corresponde. Los armónicos están separados entre sí una distancia igual a la frecuencia a la fundamental f1=1/P, y las amplitudes que les corresponden quedan limitadas por la envolvente que está dibujada con líneas de puntos. No están presentes los armónicos pares.
Figura1
Figura2
Relación entre pulsos de distintos duración y sus espectros de Fourier
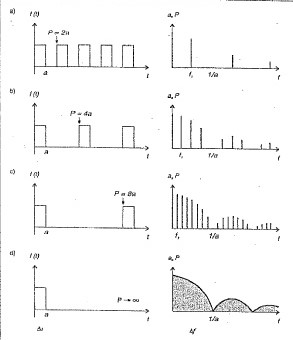
En la figura 2-b se mantiene el mismo ancho a de pulso. Pero se aumenta al doble el periodo de señal. La onda es rectangular y el espaciamiento entre armónicos se reduce a la mitad. Desaparecen el armónico 4 y sus múltiplos, aunque las amplitudes responde a la misma envolvente del caso anterior ( la envolvente responde exclusivamente de las características de cada pulso individual de ancho a, que no ah variado). En la figura 2-c se dilata mas el periodo. La señal repite recién cuando transcurre un tiempo igual a 8 veces la duración del pulso y las consecuencia en el espectro son claras; los armónicos se encuentran separados por una distancia menor y las amplitudes continúan respetando la envolvente punteada( no están presentes los armónicos múltiplos de 8 como corresponde a una señal rectangular con P=8 a).
Si aumentamos los periodos , los armónicos estarían cada vez más cerca uno de otros y se conservaría la envolvente de amplitud. Por ejemplo: en la figura 2-d se ah graficado esta señal y su espectro. La fundamental de fourier que le corresponde es f1=1/∞=0 Hz y la separación entre armónicos también es cero. Bajo la envolvente ya no hay armónicos representados por líneas, sino una banda continua que en su interior contiene un conjunto denso (infinito) de frecuencias. El golpe de tambor y cualquier otra señal limitada en el tiempo tiene un espectro de bandas parecidas. La relación que vincula las manifestaciones en el tiempo y en las frecuencias de estas señales toma el nombre de Transformada o Integral de Fourier. En síntesis las señales limitadas en el tiempo posee ancho de banda y los espectros de líneas , armónicos o no, corresponden a señales no limitas en el tiempo. Los espectros de banda no pueden caracterizarse como los de línea, por medio de una solo frecuencia porque poseen infinitos valores distintos. Ancho de banda ∆f definido como el intervalo existente entre dos frecuencias límite f1 y f2.
En la figura 5.3 el a posee un ancho de banda nulo, corresponde a una sinusoide de frecuencia f= 5.000 Hz . el b es el de una señal de banda angosta y el c de una banda ancha. El d tiene un ancho de banda infinito la energía se distribuye parejo en todas las frecuencias( ruido blanco). En la percepción de señales acústicas , interesa conocer el mínimo de ancho de banda que el oído puede detectar en función de la frecuencia central de la banda, limitados por el movimiento de la membrana basilar en el oído interno. Para determinar el ancho de banda se deben definir dos frecuencias límite. La amplitud de aproximadamente 0,7 de la amplitud máxima de la señal. Una vez determinados f1 y f2 el ancho de banda ∆f se calcula: ∆f =f2 y f1
Ejemplos
tremolo[2]
La parte del tambor de una bateaen la murga urg