Fourier, análisis de – ventana temporal
| Definición Breve | Ventana temporal es una función matemática que se emplea para poder analizar señales infinitas en una porción finita de tiempo |
|---|---|
| Tema | Análisis de señales |
| Subtema | Ventana temporal |
| Audio | <embed>Gérard Grisey - Périodes</embed> |
Una ventana es una función matemática que se emplea en el análisis y muestreo de señales por computadora. Dado que las señales a analizar deben ser reales, es decir, no podemos analizar una sinusoide ya que en teoría es infinita, previamente debemos aplicar la Transformada discreta de Fourier o DFT (ver Fourier, síntesis de) por sus siglas en inglés "discrete Fourier transform", herramienta matemática que nos permite delimitar un intervalo de tiempo finito, y pasar del dominio del tiempo al dominio de frecuencia de la señal. Una vez hecho esto, multiplicamos la señal por la función ventana y obtenemos de este modo los primeros segundos de ese intervalo, lo que nos permite analizar detalladamente los componentes de dicha señal. Dicho proceso se denomina windowing.
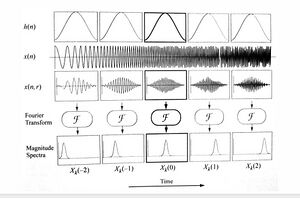
Las ventanas tienen tres propiedades: un ancho de lóbulo principal, un nivel de lóbulos laterales y una pendiente de caída. Cuanto mayor es el lóbulo principal, menor va a ser el nivel de lóbulos laterales. Los lóbulos laterales de gran magnitud producen efectos de rizado en la respuesta frecuencial del tramo de señal ventaneado.
Existen distintos tipos de ventana, y el uso de una u otra va a depender del tipo de señal a analizar, del parámetro al que se considere prioritario analizar, y en algunos casos de las posibilidades que brinde el equipo empleado para realizar tal análisis. A continuación se detallan los tipos de ventanas más comúnmente usados.
La ventana rectangular es utilizada comúnmente para analizar las señales transitorias (ver Señal no estacionaria transitoria) para conocer la presencia de eventos continuos de tipo sinusoidales.
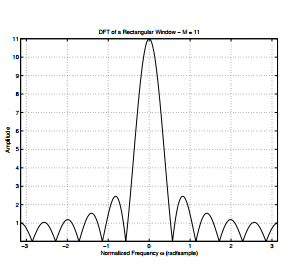
Para analizar el contenido espectral de una señal, se utiliza normalmente la ventana de Hann, ya que si bien su lóbulo principal tiene un ancho que es el doble del de la ventana rectangular, sus lóbulos laterales caen rápidamente, lo que permite resolver componentes frecuenciales cercanas.
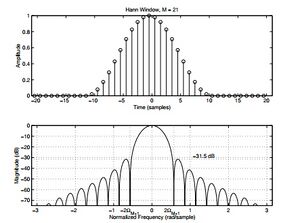
Si se desea medir la amplitud de una señal, es conveniente usar una ventana flat-top, la cual presenta un amplio lóbulo principal, y por ende la amplitud del pico espectral es muy precisa.
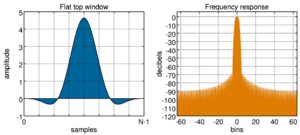
Las ventanas Gauss y Hanning se emplean para determinar eventos puntuales (se presentan en un instante fijo en todo el dominio temporal). La ventana Gauss tiene mayor utilidad sobre la ventana Hanning para separar componentes frecuenciales de niveles ampliamente diferentes. La ventana Chebyshev es útil para conocer un intervalo de componentes frecuencial y atenuar casi en su totalidad el resto de componentes y analizar señales periódicas. La ventana de Kaiser-Bessel tiende a minimizar el ancho del lóbulo principal, evitando un incremento de los lóbulos laterales.
Para hablar de la resolución en tiempo-frecuencia de la STFT (usada para determinar el contenido en frecuencia sinusoidal y de fase en secciones locales de una señal así como sus cambios con respecto al tiempo ), se requiere hablar de la selección de la ventana temporal Si la ventana seleccionada es muy estrecha se analizan segmentos de señal pequeños que permiten tener una buena resolución en tiempo pero una mala resolución en frecuencia ya que sólo se podrán observar las componentes de frecuencias igual y mayores al inverso del tamaño de la ventana. Por otro lado, si la ventana seleccionada es muy ancha se tendrá una buena resolución en frecuencia pero una mala resolución en tiempo, i.e; una ventana de ancho infinito o ancho igual al tamaño de la señal es nada más y nada menos que la TF clásica. Por lo tanto, un defecto de la STFT es el no poder dar una alta resolución tanto en tiempo como en frecuencia de manera simultánea. La raíz de este problema se basa en el principio de incertidumbre de Heisenberg , el cual establece que es imposible conocer una representación exacta tiempo-frecuencia de una señal; es decir, no podemos saber qué valor de frecuencia existe en un instante de tiempo determinado, sólo podemos conocer qué componentes de frecuencia existen dentro de un intervalo de tiempo dado. Las ventanas desplazadas y moduladas g(t-τ) e-jωt de la ecuación están bien localizadas en el dominio conjunto tiempo-frecuencia. Cada ventana se localiza en el rectángulo centrado en el punto (τ, f) con dimensión igual a ΔtΔf. Por lo anterior, es importante determinar la relación ideal entre el ancho temporal y frecuencial de la ventana en función de la exigencia del análisis que se pretenda realizar.
En el siguiente video, podemos observar cómo se realiza el análisis de una señal tanto en el dominio del tiempo como en el de frecuencia, para lo cual se emplea la Transformada de Fourier. Se está analizando un intervalo de tiempo finito para una señal del tipo "diente de sierra" (ver Onda diente de sierra)
Provided ID could not be validated.
Este es otro ejemplo del análisis a señales, en este caso una forma de onda "cuadrada" (ver Onda cuadrada), obtenido mediante el ventaneo a un intervalo de tiempo finito.
Provided ID could not be validated.
En ambos casos podemos observar, al final, los gráficos espectrales resultantes del ventaneo.
Ejemplo musical
La música espectral o Espectralismo surgida en Francia en la década de 1960 explotó el análisis de señales sonoras y la descomposición de las mismas mediante el uso de computadoras para la creación de piezas musicales. Básicamente lo que se trata de hacer es analizar las señales para poder modificar luego sus componentes armónicos y llevarlos al plano orquestal.
Gérard Grisey (músico espectralista) es un claro ejemplo de ello. En Périodes podemos apreciar cómo se lleva a cabo la mutación de un sonido al ser interpretado por distintos instrumentos. Esta evolución del sonido es posible ya que el análisis de Fourier y las distintas funciones empleadas, entre ellas la función ventana, permiten obtener un análisis armónico de los sonidos y manipular el comportamiento de dichos armónicos.
<embed>https://https://www.youtube.com/watch?v=Yljhvouhh2Q}}
Referencias
Procesamiento digital de señales. Capítulo 5. Universidad Nacional del Sur. 2011. Disponible en:[1]
Procesamiento digital de señales. Capítulo 11. Universidad Nacional del Sur. 2011. Disponible en:[2]
Cáceres, Juan Pablo. Análisis Espectral 1: Transformada Corta de Fourier y Ventanas. CCRMA. Stanford University. 2007. Disponible en: [3]
Carrillo González, José Camilo. Fundamentos del Análisis de Fourier. Departamento de Enxeñería Eléctrica. Escola Técnica Superior de Enxeñeiros Industriáis. Universidade de Vigo. Vigo, 2003. Disponible en: [4]
Ventana (función). Wikipedia, la enciclopedia libre. Disponible en: [5]
