Diferencia entre revisiones de «Suma de sinusoides – igual f y ᵠ»

Revisión actual - 01:10 24 oct 2016

Suma de sinusoides – igual f y ᵠ

Definición Breve	Uno de los dos casos de Suma de Sinusoides, cuando la frecuencia y la amplitud de las dos coinciden, causando una Sinusoide Resultante que combina los parámetros de las curvas involucradas.
Tema	Sinusoides
Subtema	Suma de Sinusoides
Audio	<embed>https://www.youtube.com/watch?v=2bw-w6xlGWc</embed>

Definición

Naturalmente, es necesario sumar señales acústicas, que se representan mediante una curva llamada Sinusoide. Esto nos permite observar la obtención de otra sinusoide con mayor amplitud, pero conservando la misma frecuencia de las dos que intervinieron en su creación. Esto ocurre de forma habitual en el ámbito acústico; la forma ideal de este fenómeno es cuando se utilizan sistemas lineales. Esto describe el desplazamiento de la onda resultante como la suma de los desplazamientos individuales de cada onda involucrada; dos sinusoides intervienen entre sí todo el tiempo en un ambiente cerrado.

Estudio de Caso

En este caso particular, tanto sus frecuencias (f) como sus amplitudes son coincidentes, lo que produce que se encuentren "en fase". Esto se logra cuando su f es igual y la diferencia de fase (Δφ) equivale a 0°. Por supuesto, "Δφ" es el parámetro clave en este caso particular de la suma de sinusoides que estamos analizando aquí. De esta manera, cuando Δφ = 0°, las dos curvas sinusoidales están en fase (como se mencionó más arriba), pero también la sinusoide resultante conservará una "fase inicial" y su amplitud será la sumatoria de las dos curvas involucradas. El otro caso particular de esta suma de señales acústicas es sobre la Suma de sinusoides – igual f y Δ ᵠ=180º.

Análisis del ejemplo sonoro

Durante los primeros instantes en el tiempo, el ejemplo sonoro demuestra una sinusoide principal que se escucha por encima de las demás, las cuales suenan de forma breve o ligeramente atenuadas. Todo cambia cuando el video alcanza 1 minuto y 40 segundos, ya que la sonoridad cambia para introducir otros sonidos más intensos que se revelan a partir de los 2 minutos y 7 segundos. Esos "sonidos más intensos" nombrados con anterioridad hacen su aparición a los 2 minutos y 40 segundos, que es cuando el caso de Suma de Sinusoides expuesto aquí se vuelve evidente. Para concluir, tanto las sinusoides de las voces como las mismas de los efectos de sonido se suman para producir sinusoides más amplias, tal cual se muestra en esta explicación

Notas

"Δ": Letra griega Delta mayúscula. Se utiliza en diversas ciencias como la "variación", "diferencia" o "intervalo", según qué variable corresponda modificarse.
"φ": Letra griega Phi minúscula. Para expresar la "fase" de una sinusoide, se utiliza esta letra para realizar los cambios a la variable que representa la fase per se.
- Ej.: En combinación con "Δ", podemos hacer los cálculos necesarios para obtener la "diferencia de fase".

Referencia

"Análisis Espectral, la Transformada de Fourier en la Música", de Gustavo Basso (Págs, 37 y 38).

@@ Línea 1: / Línea 1: @@
-{{ Conceptos de Acústica | definiciónbreve = definición breve | tema = Sinusoides | subtema = Suma de Sinusoides | imagen1 = imagenxx1xx.jpg | imagen2 = imagenxx2xx.jpg | sonido = link web al ejemplo sonoro }}
+{{ Conceptos de Acústica | definiciónbreve = Uno de los dos casos de Suma de Sinusoides, cuando la frecuencia y la amplitud de las dos coinciden, causando una Sinusoide Resultante que combina los parámetros de las curvas involucradas. | tema = Sinusoides | subtema = Suma de Sinusoides | imagen1 = Suma_general.jpg | imagen2 = Suma_caso1.jpg | sonido = https://www.youtube.com/watch?v=2bw-w6xlGWc }}
-Editado por Rubén Darío Francisco Fernández
+==Definición==
+Naturalmente, es necesario sumar señales acústicas, que se representan mediante una curva llamada [[Sinusoide]]. Esto nos permite observar la obtención de otra sinusoide con mayor amplitud, pero conservando la misma frecuencia de las dos que intervinieron en su creación. Esto ocurre de forma habitual en el ámbito acústico; la forma ideal de este fenómeno es cuando se utilizan sistemas lineales. Esto describe el desplazamiento de la onda resultante como la suma de los desplazamientos individuales de cada onda involucrada; dos sinusoides intervienen entre sí todo el tiempo en un ambiente cerrado.
+===Estudio de Caso===
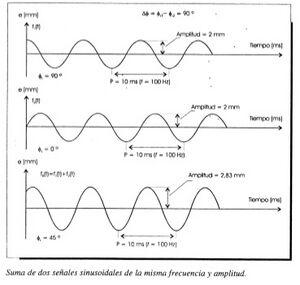
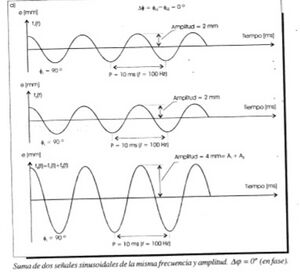
+En este caso particular, tanto sus frecuencias (f) como sus amplitudes son coincidentes, lo que produce que se encuentren "en fase". Esto se logra cuando su f es igual y la diferencia de fase (Δφ) equivale a 0°. Por supuesto, "Δφ" es el parámetro clave en este caso particular de la suma de sinusoides que estamos analizando aquí.
+De esta manera, cuando Δφ = 0°, las dos curvas sinusoidales están en fase (como se mencionó más arriba), pero también la sinusoide resultante conservará una "fase inicial" y su amplitud será la sumatoria de las dos curvas involucradas. El otro caso particular de esta suma de señales acústicas es sobre la [[Suma de sinusoides – igual f y Δ ᵠ=180º]].
+===Análisis del ejemplo sonoro===
+Durante los primeros instantes en el tiempo, el ejemplo sonoro demuestra una sinusoide principal que se escucha por encima de las demás, las cuales suenan de forma breve o ligeramente atenuadas. Todo cambia cuando el video alcanza 1 minuto y 40 segundos, ya que la sonoridad cambia para introducir otros sonidos más intensos que se revelan a partir de los 2 minutos y 7 segundos. Esos "sonidos más intensos" nombrados con anterioridad hacen su aparición a los 2 minutos y 40 segundos, que es cuando el caso de Suma de Sinusoides expuesto aquí se vuelve evidente. Para concluir, tanto las sinusoides de las voces como las mismas de los efectos de sonido se suman para producir sinusoides más amplias, tal cual se muestra en esta explicación
+----
+===Notas===
+*"Δ": Letra griega Delta mayúscula. Se utiliza en diversas ciencias como la "variación", "diferencia" o "intervalo", según qué variable corresponda modificarse.
+*"φ": Letra griega Phi minúscula. Para expresar la "fase" de una sinusoide, se utiliza esta letra para realizar los cambios a la variable que representa la fase per se.
+**Ej.: En combinación con "Δ", podemos hacer los cálculos necesarios para obtener la "diferencia de fase".
+----
+==Referencia==
+"''Análisis Espectral, la Transformada de Fourier en la Música''", de Gustavo Basso (Págs, 37 y 38).
+[[Category: Conceptos de acústica]]