Diferencia entre revisiones de «Sinusoide»
Sin resumen de edición |
Sin resumen de edición |
||
| Línea 5: | Línea 5: | ||
Las ondas sonoras forman un espectro de longitudes de onda. La mayoría de los sonidos son ondas dentadas y complejas, pero existen unas ondas en particular, que se grafican en una '''sinusoide'''. Es una oscilación repetitiva en el cual la frecuencia no posee armonía, y que por medio de ondas sinusoidales, se puede ver lo que es el '''período''', '''amplitud''', '''frecuencia''', '''amplitud''' y '''ciclo'''. | Las ondas sonoras forman un espectro de longitudes de onda. La mayoría de los sonidos son ondas dentadas y complejas, pero existen unas ondas en particular, que se grafican en una '''sinusoide'''. Es una oscilación repetitiva en el cual la frecuencia no posee armonía, y que por medio de ondas sinusoidales, se puede ver lo que es el '''período''', '''amplitud''', '''frecuencia''', '''amplitud''' y '''ciclo'''. | ||
Antes de definir lo que es una señal sinusoidal, vamos a definir lo que es una señal en nuestro campo de estudio ya sea musical, sonoro o visual , señal es una variación en el tiempo o espacio de una [https://es.wikipedia.org/wiki/Magnitud_f%C3%ADsica magnitud fisica] o de otra naturaleza. | Antes de definir lo que es una señal sinusoidal, vamos a definir lo que es una señal en nuestro campo de estudio ya sea musical, sonoro o visual , señal es una variación en el tiempo o espacio de una [https://es.wikipedia.org/wiki/Magnitud_f%C3%ADsica magnitud fisica] o de otra naturaleza. | ||
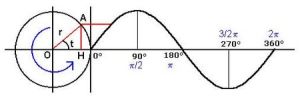
Definamos sinusoide segun RAE (del latin sinus, seno y el griego eidos forma) física geometría, curva plana, cuya ordenada es el https://es.wikipedia.org/wiki/Seno_(trigonometr%C3%ADa) del arco que tiene por radio a la https://es.wikipedia.org/w/index.php?title=Abscisa&redirect=no | Definamos sinusoide segun RAE (del latin sinus, seno y el griego eidos forma) física geometría, curva plana, cuya ordenada es el [https://es.wikipedia.org/wiki/Seno_(trigonometr%C3%ADa) seno] del arco que tiene por radio a la [https://es.wikipedia.org/w/index.php?title=Abscisa&redirect=no abscisa] la misnma misma curva. | ||
==Ejemplo=={{YouTube| https://youtu.be/_FaZdasMuqM }} | ==Ejemplo=={{YouTube| https://youtu.be/_FaZdasMuqM }} | ||
Revisión del 22:55 30 sep 2017
| Definición Breve | La sinusoide es el ejemplo matemático fundamental en la acústica, que sirve para demostrar el movimiento de las ondas. Onda sinusoide es una clase particular de onda regularmente curva que describe el comportamiento de los tipos más simples de sistemas oscilantes. Los tonos musicales puros o las señales eléctricas producen ondas sinusoidales. |
|---|---|
| Tema | movimiento armónico simple señales acústicasLa propiedad «Acústica» (como tipo de página) con el valor de entrada «movimiento armónico simple</br>señales acústicas» contiene caracteres inválidos o está incompleto, por lo que puede causar resultados inesperados durante una consulta o proceso de anotación. |
| Subtema | señal sinusoidal |
| Audio | <embed>https://www.youtube.com/watch?v=qNf9nzvnd1k</embed> |
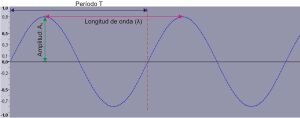
Las ondas sonoras forman un espectro de longitudes de onda. La mayoría de los sonidos son ondas dentadas y complejas, pero existen unas ondas en particular, que se grafican en una sinusoide. Es una oscilación repetitiva en el cual la frecuencia no posee armonía, y que por medio de ondas sinusoidales, se puede ver lo que es el período, amplitud, frecuencia, amplitud y ciclo.
Antes de definir lo que es una señal sinusoidal, vamos a definir lo que es una señal en nuestro campo de estudio ya sea musical, sonoro o visual , señal es una variación en el tiempo o espacio de una magnitud fisica o de otra naturaleza.
Definamos sinusoide segun RAE (del latin sinus, seno y el griego eidos forma) física geometría, curva plana, cuya ordenada es el seno del arco que tiene por radio a la abscisa la misnma misma curva.
Ejemplo
Provided ID could not be validated.
Provided ID could not be validated.
En el ejemplo, se puede ver claramente cómo a medida que la frecuencia va subiendo, el movimiento de las ondas se hace más rápido, la longitud de las ondas empieza a disminuir, la amplitud aumenta, y el período (tiempo en completar un ciclo, medido en segundos) empieza a disminuir, es decir que un ciclo se completa más rápido.
Provided ID could not be validated.
Del minuto 0:19 al 0:30, se puede escuchar un sampler que va en aumento y llega a su punto máximo en la canción. Se puede tomar como ejemplo, ya que si se viera un gráfico de ese sampler, se vería cómo las ondas aumentan de velocidad, y se encuentran cada vez más cerca una de la otra.