Diferencia entre revisiones de «Sinusoide»
(Video de onda sinusoidal) |
Sin resumen de edición |
||
| Línea 3: | Línea 3: | ||
señales acústicas | subtema = señal sinusoidal | imagen1 = Sinusoide.jpg | imagen2 = Image011.jpg | sonido = https://www.youtube.com/watch?v=qNf9nzvnd1k}} | señales acústicas | subtema = señal sinusoidal | imagen1 = Sinusoide.jpg | imagen2 = Image011.jpg | sonido = https://www.youtube.com/watch?v=qNf9nzvnd1k}} | ||
==Introduccion== | |||
Antes de definir lo que es una señal sinusoidal, vamos a definir lo que es una señal en nuestro campo de estudio ya sea musical, sonoro o visual , señal es una variación en el tiempo o espacio de una [https://es.wikipedia.org/wiki/Magnitud_f%C3%ADsica magnitud fisica] o de otra naturaleza. | Antes de definir lo que es una señal sinusoidal, vamos a definir lo que es una señal en nuestro campo de estudio ya sea musical, sonoro o visual , señal es una variación en el tiempo o espacio de una [https://es.wikipedia.org/wiki/Magnitud_f%C3%ADsica magnitud fisica] o de otra naturaleza. | ||
Definamos sinusoide | Definamos sinusoide según RAE (del latin sinus, seno y el griego eidos forma) física geometría, curva plana, cuya ordenada es el [https://es.wikipedia.org/wiki/Seno_(trigonometr%C3%ADa) seno] del arco que tiene por radio a la [https://es.wikipedia.org/w/index.php?title=Abscisa&redirect=no abscisa] la misma curva. | ||
Fue el matemático francés [http://forohistorico.coit.es/index.php/personajes/personajes-internacionales/item/fourier-jean-baptiste-joseph fourier jean baptiste joseph], a principios del siglo XIX,quien encontró que una función periódica se puede representar como una suma infinita ponderada de términos en senos y cosenos(la serie de Fourier) todas las señales cualquiera sea su origen se analizar con el método [http://Fourier,_an%C3%A1lisis_de Fourier] | |||
==Ejemplo== | ==Ejemplo 1== | ||
Animación de una onda sinusoidal | Animación de una onda sinusoidal | ||
{{YouTube| https://youtu.be/_FaZdasMuqM }} | {{YouTube| https://youtu.be/_FaZdasMuqM }} | ||
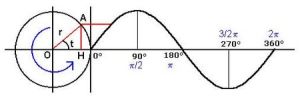
La onda sinusoidal es una señal simple, una sola señal un tono puro una única frecuencia, es periódica e infinita, no tiene principio ni tiene fin, toma el nombre según donde se dibuje la onda, puede ser senoidales que comienza en cero o coseidales que comienza a dibujar la señal en el valor máximo, igualmente puede ser proyectada desde cualquier punto y seguiría siendo sinusoidal. La porción mínima de una onda sinusoidal se denomina ciclo y el [[Periodo|periodo]] es el resultado de el tiempo que tarda el ciclo en ser repetido. Las ondas sinusoidales se utilizan para representar funciones de [https://es.wikipedia.org/wiki/Onda_sonora onda sonora] y las ondas de corriente alterna. | ==Definición== | ||
La onda sinusoidal es una señal analógica simple, una sola señal un tono puro una única frecuencia, es periódica e infinita, no tiene principio ni tiene fin, toma el nombre según donde se dibuje la onda, puede ser senoidales que comienza en cero o coseidales que comienza a dibujar la señal en el valor máximo, igualmente puede ser proyectada desde cualquier punto y seguiría siendo sinusoidal. La porción mínima de una onda sinusoidal se denomina ciclo y el [[Periodo|periodo]] es el resultado de el tiempo que tarda el ciclo en ser repetido. Las ondas sinusoidales se utilizan para representar funciones de [https://es.wikipedia.org/wiki/Onda_sonora onda sonora] y las ondas de corriente alterna. | |||
[[Archivo:Onda-01.jpg|miniaturadeimagen|centro|Gráfico]] | [[Archivo:Onda-01.jpg|miniaturadeimagen|centro|Gráfico]] | ||
<embedvideo service="youtube">https://www.youtube.com/watch? | <embedvideo service="youtube">https://www.youtube.com/watch? | ||
v=qNf9nzvnd1khttps://youtu.be/_FaZdasMuqM</embedvideo> | v=qNf9nzvnd1khttps://youtu.be/_FaZdasMuqM</embedvideo> | ||
==Características== | |||
Las señales sinusoidales tiene características que son las siguientes [[Amplitud|amplitud]], [[Frecuencia|frecuencia]],[[Fase|fase]].También las señales sinusoidales se pueden [http://Suma_de_sinusoides_%E2%80%93_igual_f_y_%E1%B5%A0 sumar ] | Las señales sinusoidales tiene características que son las siguientes [[Amplitud|amplitud]], [[Frecuencia|frecuencia]],[[Fase|fase]].También las señales sinusoidales se pueden [http://Suma_de_sinusoides_%E2%80%93_igual_f_y_%E1%B5%A0 sumar ] | ||
=Ejemplo 2= | |||
{{YouTube| https://youtu.be/hFkhPOdIUJ8 }} | {{YouTube| https://youtu.be/hFkhPOdIUJ8 }} | ||
Ejemplo | |||
==Ejemplo 3== Como graficar una onda sinusoidal | |||
{{YouTube| https://youtu.be/cbU77mtipjk }} | {{YouTube| https://youtu.be/cbU77mtipjk }} | ||
==Ejemplo 4== una señal sinusoidal, visualizar un sonidos puro | |||
{{YouTube|https://youtu.be/qNf9nzvnd1k }} | {{YouTube|https://youtu.be/qNf9nzvnd1k }} | ||
| Línea 35: | Línea 45: | ||
En el ejemplo, se puede ver claramente cómo a medida que la frecuencia va subiendo, el movimiento de las ondas se hace más rápido, la longitud de las ondas empieza a disminuir, la amplitud aumenta, y el período (tiempo en completar un ciclo, medido en segundos) empieza a disminuir, es decir que un ciclo se completa más rápido. | En el ejemplo, se puede ver claramente cómo a medida que la frecuencia va subiendo, el movimiento de las ondas se hace más rápido, la longitud de las ondas empieza a disminuir, la amplitud aumenta, y el período (tiempo en completar un ciclo, medido en segundos) empieza a disminuir, es decir que un ciclo se completa más rápido. | ||
{{YouTube| {{YouTube| ID del video }} }} | {{YouTube| {{YouTube| ID del video }} }} | ||
==Ejemplo 5 musical== Aplicación de una onda sinusoidal utilizada por un teclado sintetizador | |||
{{YouTube|https://youtu.be/EmR5oZRuRqg }} | |||
Del minuto 0:19 al 0:30, se puede escuchar un sampler que va en aumento y llega a su punto máximo en la canción. Se puede tomar como ejemplo, ya que si se viera un gráfico de ese sampler, se vería cómo las ondas aumentan de velocidad, y se encuentran cada vez más cerca una de la otra. | Del minuto 0:19 al 0:30, se puede escuchar un sampler que va en aumento y llega a su punto máximo en la canción. Se puede tomar como ejemplo, ya que si se viera un gráfico de ese sampler, se vería cómo las ondas aumentan de velocidad, y se encuentran cada vez más cerca una de la otra. | ||
==Ejemplo 6== de ondas sinusoidales con elementos muy cotidianas para los músicos | |||
{{YouTube| https://youtu.be/YRv4POv5jh4 }} | {{YouTube| https://youtu.be/YRv4POv5jh4 }} | ||
==Ejemplo 7== una armónica de cristal genera una onda sinusoidal casi pura junto con en piapason. | |||
{{YouTube|https://youtu.be/eQemvyyJ--g }} | |||
Por ultimo, acá se puede apreciar una onda sinusoidal en un hilo de algodón: | Por ultimo, acá se puede apreciar una onda sinusoidal en un hilo de algodón: | ||
| Línea 64: | Línea 82: | ||
*https://youtu.be/hFkhPOdIUJ8 | *https://youtu.be/hFkhPOdIUJ8 | ||
*https://youtu.be/qNf9nzvnd1k | *https://youtu.be/qNf9nzvnd1k | ||
*https://youtu.be/eQemvyyJ--g | |||
[[Category: Conceptos de acústica]] | [[Category: Conceptos de acústica]] | ||
Revisión del 01:59 2 oct 2017
| Definición Breve | La sinusoide es el ejemplo matemático fundamental en la acústica, que sirve para demostrar el movimiento de las ondas. Onda sinusoide es una clase particular de onda regularmente curva que describe el comportamiento de los tipos más simples de sistemas oscilantes. Los tonos musicales puros o las señales eléctricas producen ondas sinusoidales. |
|---|---|
| Tema | movimiento armónico simple señales acústicasLa propiedad «Acústica» (como tipo de página) con el valor de entrada «movimiento armónico simple</br>señales acústicas» contiene caracteres inválidos o está incompleto, por lo que puede causar resultados inesperados durante una consulta o proceso de anotación. |
| Subtema | señal sinusoidal |
| Audio | <embed>https://www.youtube.com/watch?v=qNf9nzvnd1k</embed> |
Introduccion
Antes de definir lo que es una señal sinusoidal, vamos a definir lo que es una señal en nuestro campo de estudio ya sea musical, sonoro o visual , señal es una variación en el tiempo o espacio de una magnitud fisica o de otra naturaleza. Definamos sinusoide según RAE (del latin sinus, seno y el griego eidos forma) física geometría, curva plana, cuya ordenada es el seno del arco que tiene por radio a la abscisa la misma curva. Fue el matemático francés fourier jean baptiste joseph, a principios del siglo XIX,quien encontró que una función periódica se puede representar como una suma infinita ponderada de términos en senos y cosenos(la serie de Fourier) todas las señales cualquiera sea su origen se analizar con el método Fourier
Ejemplo 1
Animación de una onda sinusoidal
Provided ID could not be validated.
Definición
La onda sinusoidal es una señal analógica simple, una sola señal un tono puro una única frecuencia, es periódica e infinita, no tiene principio ni tiene fin, toma el nombre según donde se dibuje la onda, puede ser senoidales que comienza en cero o coseidales que comienza a dibujar la señal en el valor máximo, igualmente puede ser proyectada desde cualquier punto y seguiría siendo sinusoidal. La porción mínima de una onda sinusoidal se denomina ciclo y el periodo es el resultado de el tiempo que tarda el ciclo en ser repetido. Las ondas sinusoidales se utilizan para representar funciones de onda sonora y las ondas de corriente alterna.
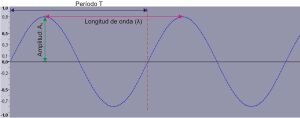
Características
Las señales sinusoidales tiene características que son las siguientes amplitud, frecuencia,fase.También las señales sinusoidales se pueden sumar
Ejemplo 2
Provided ID could not be validated.
==Ejemplo 3== Como graficar una onda sinusoidal
Provided ID could not be validated.
==Ejemplo 4== una señal sinusoidal, visualizar un sonidos puro
Provided ID could not be validated.
En el ejemplo, se puede ver claramente cómo a medida que la frecuencia va subiendo, el movimiento de las ondas se hace más rápido, la longitud de las ondas empieza a disminuir, la amplitud aumenta, y el período (tiempo en completar un ciclo, medido en segundos) empieza a disminuir, es decir que un ciclo se completa más rápido.
Provided ID could not be validated.
==Ejemplo 5 musical== Aplicación de una onda sinusoidal utilizada por un teclado sintetizador
Provided ID could not be validated.
Del minuto 0:19 al 0:30, se puede escuchar un sampler que va en aumento y llega a su punto máximo en la canción. Se puede tomar como ejemplo, ya que si se viera un gráfico de ese sampler, se vería cómo las ondas aumentan de velocidad, y se encuentran cada vez más cerca una de la otra.
==Ejemplo 6== de ondas sinusoidales con elementos muy cotidianas para los músicos
Provided ID could not be validated.
==Ejemplo 7== una armónica de cristal genera una onda sinusoidal casi pura junto con en piapason.
Provided ID could not be validated.
Por ultimo, acá se puede apreciar una onda sinusoidal en un hilo de algodón:
<iframe width="560"height="315"src="https://www.youtube.com/embed/BTCZmOpCxtI"frameborder="0"allowfullscreen></iframe>
Referencias
- https://es.wikipedia.org/wiki/Sinusoide
- http://www.domingo-roman.net/acusticabasica.html
- http://www.gradomultimedia.com/29-musica/1_1-las-ondas.html
- Gustavo Basso (Análisis espectral, Colección Universitaria de la Universidad de La Plata, 2001)
- https://es.wikipedia.org/wiki/Magnitud_f%C3%ADsica
- http://musiki.org.ar/Amplitud
- http://musiki.org.ar/Fase
- http://musiki.org.ar/Frecuencia
- http://musiki.org.ar/Periodo
- RAE diccionario de la real española
- https://youtu.be/cbU77mtipjk
- http://forohistorico.coit.es/index.php/personajes/personajes-internacionales/item/fourier-jean-baptiste-josep
- https://youtu.be/YRv4POv5jh4
- https://youtu.be/_FaZdasMuqM
- https://youtu.be/hFkhPOdIUJ8
- https://youtu.be/qNf9nzvnd1k
- https://youtu.be/eQemvyyJ--g