Profundidad de bits

Definición Breve	Es la resolución, en terminos de amplitud de onda, que va a tener una señal digitalizada. Determina el rango dinámico que tiene dicha señal.
Tema	Audio Digital
Subtema	Profundidad de Bits
Audio	<embed>Ben Landis - Breakthrough</embed>

Definición

En audio digital la profundidad de bits es el numero de bits de información de cada muestra y esta estrechamente ligado a la resolución del audio. A diferencia de una señal analógica, la cual es periódica y esta compuesta por infinitos puntos, el audio digital es una señal discreta ya que esta compuesta por un número finito de puntos. Usa números binarios (bits) para determinar la cantidad de estados disponibles para representar la fuerza de cada muestra de audio y así representar la señal. "La calidad de la representación aumenta, en general, cuando se incrementa este número de estados. Por ejemplo, [...] la grabación de música de alta fidelidad se obtiene en un CD con 65.536 niveles de amplitud. La cantidad de estados posibles de un sistema binario de n dígitos (n bits) es E=2^n." 1. En resumen, es la resolución, en terminos de amplitud, que va a tener una señal digitalizada. Determina el rango dinámico que tiene dicha señal. En la siguiente imagen podemos ver como está representada una señal en 4 bits de profundidad. 4 bits generan 16 valores posibles en el eje vertical.

Errores de cuantización

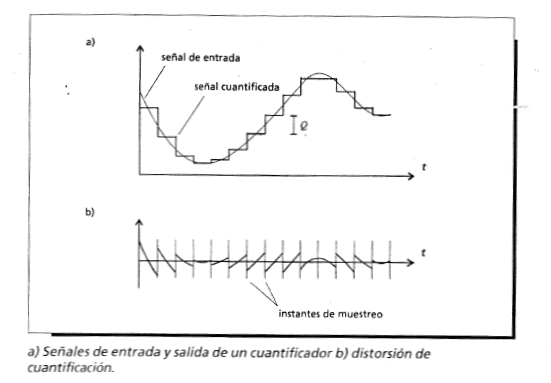
A grandes rasgos, el proceso de cuantificación le asigna un valor discreto a las amplitudes de cada una de las muestras obtenidas en la etapa de muestreo. "Para convertirla en una señal digital la amplitud debe ser cuantificada en un número determinado de escalones (quanta). La cantidad infinita de puntos de una onda analógica será representada por una cantidad finita de estados: claramente, se introduce un error."2. Estos errores resultan de igualar los niveles de las muestras de amplitud continua a los niveles de cuantificación mas proximos. En la siguiente imagen, tomada del libro "Análisis Espectral. La transformada de Fourier en la música", podemos ver una representación de una señal cuantificada.

"La minima diferencia analógica Q que puede resolver un conversor [analógico-digital] establece el menor de los escalones de la figura. Q depende de la amplitud maxima entre picos o Rango de la señal muestreada y de la cantidad de estados posibles del sistema [...]". "Se ve claramente que a medida que crece el número de bits se reduce el escalon mínimo (o resolución) del sistema. El valor de Q define el error o ruido de cuantificación que se ha dibujado por separado [en la imagen superior]"3. En resumen, el proceso de conversión analógico-digital le va a agregar a la señal ruido de cuantificación. Este ruido posee un gran ancho de banda y se comporta como una distorsion de la señal. Se lo oye como "ruido detras de la señal" y contribuye a la distorsión total en cualquier sistema de audio digital.

Aspectos a tener en cuenta

La precisión de cada muestra esta determinada por su profundidad de bits. Entonces, a mayor profundidad de bits mayor resolución en la señal digitalizada. Además, a mayor profundidad de bits mayor rango dinámico para la señal debido a que va a tener mas puntos para representar la amplitud de cada muestra de audio. De esto se desprende que bajos niveles de profundidad de bits pueden llegar a afectar la forma de la onda y así no lograr una buena representación de la onda original debido a que hay menos puntos posibles para representarla. Por ejemplo, en el siguiente gráfico podemos ver una sinusoide representada con diferentes profundidades de bits. Una profundidad de 1 bit nos va a generar una onda mas parecida a la onda cuadrada (dependiendo de la cuantificación) debido a que solo tenemos dos puntos posibles en el eje vertical.

Requerimientos

Un aspecto muy importante a tener en cuenta es que a mayor profundidad de bits vamos a necesitar mas recursos para procesar el audio y mas memoria para guardarlo. Esto se debe a que vamos a tener mas información. El tamaño de nuestro archivo de audio va a estar dado por la siguiente cuenta:

Número bits * Frecuencia de muestreo * cantidad de segundos de duración [* 2 (si es una señal stereo)]

Entonces, por ejemplo, el tamaño de un segundo de audio en un CD, que trabaja con una profundidad de 16 bits y una frecuencia de muestreo de 44.100Hz/segundo va a estar dado por la siguiente cuenta:

1 segundo = 16 * 44100 * 2 (ya que es stereo)

1 segundo = 1411200 bits (0,1764 Mb)

Comparando diferentes profundidades de bits

En el siguiente cuadro podemos comparar el rango dinámico (en decibeles) y cantidad de valores posibles de amplitud de una señal digitalizada con diferentes profundidades de bits.

Aplicaciones

Estos son algunos sistemas de audio digital que trabajan con diferentes profundidades de bits.

Ejemplo Sonoro

En el ejemplo musical se puede escuchar una obra de Ben Landis, el cual es un productor musical que se especializa en el genero musical Chiptune. Las características principales de dicho genero tienen que ver con el uso de sonidos generados por chips de sonido PSG (Programmable sound generator). Los cuales eran usados en computadoras y consolas de videojuegos antiguas. Actualmente, además de usar los chips de sonido PSG los artistas suelen usar emuladores que producen sonidos similares. Una de las características principales de estos sistemas es que trabajan con señales que tienen profundidades de bits menores a las que estamos mas acostumbrados a escuchar, por ejemplo, los CDs tienen 16 bits y los DVDs 24 bits. Generalmente, estos chips trabajan con señales de una profundidad de 8 bits. Solo de esta forma se logran los timbres, texturas y estéticas que definen el genero Chiptune.

Provided ID could not be validated.

Obviamente, a mayor cantidad de bits, mayores Estados son posibles. En el siguiente ejemplo se comparan dos piezas musicales, llevándolas hacia una transición de 16-bits a 4-bits. La primer pieza trabaja con más profundidad, y la transición es mucho más notoria, el resultado en 4-bits se percibe el efecto de "aliasing". En la segunda pieza se utilizan menos rango dinámico, por lo que la transición que sufre es casi imperceptible al oído.

Provided ID could not be validated.

En este ejemplo podemos escuchar un mismo track de audio siendo procesado de tal forma que varíe su profundidad de bits desde 16 hasta 4. A medida que baja su resolución, hay menor cantidad de Estados que permitan tomar muestreos del audio original. Esto quiere decir que hay menos información disponible y en los vacíos se rellena el sonido con señales de ruido.

https://soundcloud.com/jeremias-monardes-lagrana/bit-depth-izotope-pro-audio-essentials/s-UhI1u

Referencias

Libro: "Análisis Espectral. La transformada de Fourier en la música". Gustavo Basso. Capitulo VI: "Aplicaciones del análisis espectral". Apartado de Digitalización de señales.

https://en.wikipedia.org/wiki/Audio_bit_depth

http://www.unimusica-peru.com/produccion_musical_profundidad_bits.htm

https://en.wikipedia.org/wiki/Chiptune

http://music.stackexchange.com/

1 - G. Basso. "Análisis Espectral. La transformada de Fourier en la música". Capitulo VI: "Aplicaciones del análisis espectral". Página 186.

2 - G. Basso. "Análisis Espectral. La transformada de Fourier en la música". Capitulo VI: "Aplicaciones del análisis espectral". Página 186.

3 - G. Basso. "Análisis Espectral. La transformada de Fourier en la música". Capitulo VI: "Aplicaciones del análisis espectral". Página 191.